Modelling interactions between waves and diffused interfaces

Abstract

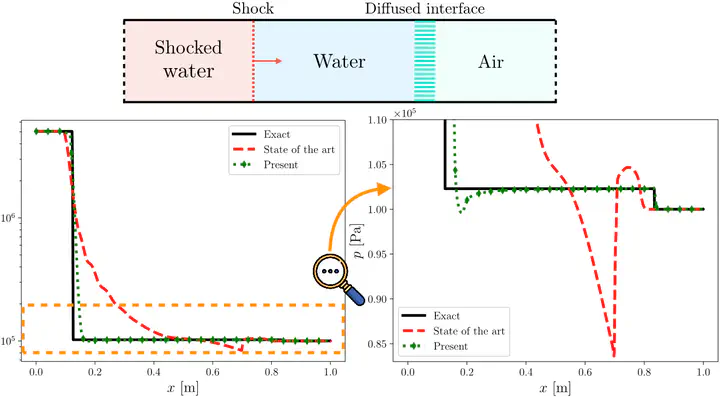
When simulating multiphase compressible flows using the diffuse-interface methods, the test cases presented in the literature to validate the modellings with regard to interface problems are always textbook cases, interfaces are sharp and the simulations therefore easily converge to the exact solutions. In real problems, it is rather different because the waves encounter moving interfaces which consequently have already undergone the effects of numerical diffusion. Numerical solutions resulting from the interactions of waves with diffused interfaces have never been precisely investigated and for good reasons, the results obtained are extremely dependent on the model used. Precisely, well-posed models present similar and important issues when such an interaction occurs, coming from the appearance of a wave-trapping phenomenon. To circumvent those issues, we propose to use a thermodynamically-consistent pressure-disequilibrium model with finite, instead of infinite, pressure-relaxation rate to overcome the difficulties inherent in the computation of these interactions. Because the original method to solve this model only enables infinite relaxation, we propose a new numerical method allowing infinite as well as finite relaxation rates. Solutions of the new modelling are examined and compared to literature, in particular we propose the study of a shock on a water–air interface, but also for problems of helium–air and water–air shock tubes, spherical and non-spherical bubble collapses.